范畴论完全装逼手册 / Grokking Monad
第二部分:食用猫呢

“If I had a world of my own, everything would be nonsense. Nothing would be what it is, because everything would be what it isn't. And contrary wise, what is, it wouldn't be. And what it wouldn't be, it would. You see?” ― Lewis Carroll, Alice's Adventures in Wonderland & Through the Looking-Glass
如果有一个单子的世界, 那一切都说不通了. 没有什么是应该的, 因为所有东西都是它不是的东西. 反过来说, 是又不会是, 而不会是的又会是. 懂没?
到底什么是, 什么不是, 我们看编程世界里到底什么是单子?
这一部分将介绍由一些实用的单子实例,通过这些单子实例,解决了分离计算与副作用, 已经组合性的问题。
Identity 本身就有 从来没见过有人给这些数据类型按过中文名字, 不然我来, 这样也更好的体会这些数据类型的意图.
本身就有单子 可能是最简单的单子了。本身不包含任何计算, 且只有一个构造器:
newtype Identity a = Identity { runIdentity :: a }
case class Identity[A](run: A)
这里使用 newtype 而不是 data 是因为 Identity 与 runIdentity 是同构的
见 第一部分 伴随函子
.
Identity :: a -> Identity a
runIdentity :: Identity a -> a
你看 runIdentity . Identity = id ,所以他们是同构的。
左边的 Identity 是类型构造器
也就是 Kind * -> *, 因为它非常的 nice, 一定要等到 a 才出类型
, 接收类型 a 返回 Identity a 类型
如果 a 是 Int,那么就得到一个 Identity Int 类型。
右边的 Identity 是数据构造器,也就是构造值,比如 Identity 1 会构造出一个值,其类型为 Identity Int
大括号比较诡异,可以想象成给 a 一个 key,同过这个 key 可以把 a 取出来,比如
runIdentity (Identity 1)
1
Identity(1).run
会返回 1
Identity 可以实现 Functor 和 Monad,就得到 Identity functor 和 Identity monad:
instance Functor Identity where
fmap f (Identity a) = Identity (f a)
instance Monad Identity where
return a = Identity a
Identity a >>= f = f a
而 Scala 则需要用 implicit 来实现 typeclass:
implicit val identityFunctor: Functor[Identity] = new Functor[Identity] {
def fmap[A, B](f: A => B): Identity[A] => Identity[B] = {
case Identity(a) => Identity(f(a))
}
}
implicit val identityMonad: Monad[Identity] = new Monad[Identity] {
def pure[A](a: A): Id[A] = Identity(a)
def flatMap[A, B](f: A => Identity[B]): Identity[A] => Identity[B] = {
case Identity(a) => f(a)
}
}
可以看到 Identity 即是构造器,也是解构器,利用模式匹配是可以解构出值的。
例如上面 Functor 实现中的 fmap f (Identity a), 假如 fmap 的是 Identity 1,
那么这个模式匹配到 (Identity a) 时会通过解构器把 1 放到 a 的位置。
Identity 看起来什么也没有干,就跟 identity 函数一样,但是实际上, 它也跟 identity 相对于函数一样 相对于类型非常有用.
Maybe 可能会有
可能会有单子是一个超级简单的但比本身就有稍稍复杂的单子.
因为它拥有比本身就有多一个的类型构造器,类似这样的叫做 代数数据类型
data Maybe a = Just a | Nothing
你看, 不管是 Just 还是 Nothing 都可以构造出一个 Maybe 类型的数据来.
ADT 在 Scala 可以用 trait 表示, 而且, Scala 中的 Maybe 叫做 Option:
trait Option[+A]
case class Some[A](a: A) extends Option[A]
case object None extends Option[Nothing]
Haskell 中定义一个 ADT 十分简单,不像 Scala 那么啰嗦。左边是类型构造器,右边有数据构造器,你会发现有一根竖线 | , 它分隔着两个构造器
JustNothing
其中 a
一定要记得小写哦
表示是任意类型.
所以 Just 1 会得到一个 Num a => Mabye a 类型
意思就是 Maybe a 但是 a 的类型约束为 Num
,
Nothing 也会得到一个 Maybe a 只不过 a 没有类型约束。
总之我们有了构造器可以构造出 Maybe 类型,而这个类型能做的事情,就要取决它实现了哪些 typeclass 的 instance 了。比如它可以是一个函子.
instance Functor Maybe where
fmap f (Just a) = Just (f a)
fmap f Nothing = Nothing
implicit val optionFunctor: Functor[Option] = new Functor[Option] {
def fmap[A, B](f: A => B): Option[A] => Option[B] = {
case Some(a) => Some(f(a))
case None => None
}
}
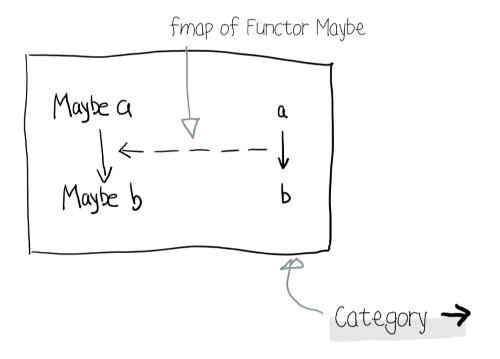
看清楚了, 虚线箭头即 fmap, 图上表示的 fmap 是 (a -> b) - - -> (Maybe a -> Maybe b) 由于这里的箭头都是在 -> 范畴, 所以 - - -> 就是 -> 了.
即: fmap :: (a -> b) -> f a -> f b
不仅如此,还可以实现单子:
instance Monad Maybe where
return a = Just a
(Just a) >>= f = f a
Nothing >>= f = Nothing
implicit val optionMonad: Monad[Option] = new Monad[Option] {
def flatMap[A, B](f: A => Option[B]): Option[A] => Option[B] = {
case Some(a) => f(a)
case None => None
}
}
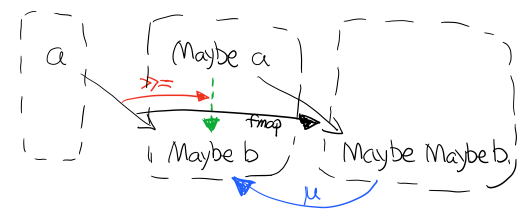
Maybe 有用在于能合适的处理 偏函数 的返回值。 偏函数相对于 全函数 是指只能对部分输入返回输出的函数。
比如一个取数组某一位上的值的函数,就是偏函数,因为假设你想取第4位的值,但不是所有数组长度都大于4,就会有获取不了的尴尬情况。
[1,2,3] !! 4
List(1,2,3).get(4)
如果使用 Maybe 把偏函数处理不了的输入都返回成 Nothing,这样结果依然保持 Maybe 类型,不影响后面的计算。
Either 要么有要么有
Either 的定义也很简单
data Either a b = Left a | Right b
trait Either[+A, +B]
case class Left[+A, +B](a: A) extends Either[A, B]
case class Right[+A, +B](b: B) extends Either[A, B]
Product & Coproduct
看过第一部分应该还能记得有一个东西叫 Duel,所以见到如果范畴上有 Coproduct 那么肯定在duel范畴上会有同样的东西叫 Product。
那么我们先来看看什么是 Coproduct
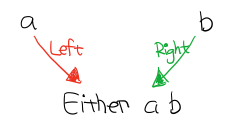
像这样,能通过两个箭头到达同一个东西,就是 Coproduct。这里箭头 Left 能让 a 到 Either a b , 箭头 Right 也能让 b 到达 Either a b
有意思的是还肯定存在一个 Coproduct 和 箭头,使得下图成立
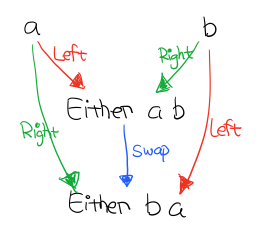
箭头反过来,就是 Product, 比如 Tuple
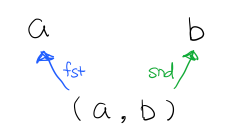
Tuple 的 fst 箭头能让 (a, b) 到达 a 对象,而箭头 snd 能让其到达 b 对象。
Either Monad
确切的说,Either 不是 monad, Either a 才是。还记得 monad 的 class 定义吗?
class Endofunctor m => Monad m where
eta :: a -> (m a)
mu :: m m a -> m a
所以 m 必须是个 Endofunctor,也就是要满足 Functor
class Functor t where
fmap :: (a -> b) -> (t a -> t b)
t a 的 kind 是 *,所以 t 必须是 kind * -> * 也就是说,m 必须是接收一个类型参数的类型构造器
而 Either 的 kind 是 * -> * -> *, Either a 才是 * -> *
所以只能定义 Either a 的 Monad
instance Monad (Either a) where
Left l >>= _ = Left l
Right r >>= k = k r
很明显的,>>= 任何函数到左边 都不会改变,只有 >>= 右边才能产生新的计算。
Reader 差一点就有
Reader 的作用是给一个计算喂数据。
在描述计算的时候,并不需要关心输入时什么,只需要 asks 就可以拿到输入值
而真正的输入,会在运行计算时给予。
跟 Identity 一样,我们用 newtype 来定义一个同构的 Reader 类型
newtype Reader e a = Reader { runReader :: (e -> a) }
其中
- e 是输入
- a 是结果
- 构造 Reader 类型需要确定 输入的类型 e 与输出的类型 a
runReader的类型是runReader:: (Reader e a) -> (e -> a)
也就是说在描述完一个 Reader 的计算后,使用 runReader 可以得到一个 e -> a 的函数,使用这个函数,就可以接收输入,通过构造好的计算,算出结果 a 返回。
那么,让我们来实现 Reader 的 monad instance,就可以描述一个可以 ask 的计算了。
instance Monad (Reader e) where
return a = Reader $ \_ -> a
(Reader g) >>= f = Reader $ \e -> runReader (f (g e)) e
跟Either一样,我们只能定义 Reader e 的 monad instance。
注意这里的
- f 类型是
(a -> Reader e a) - g 其实就是是 destructure 出来的 runReader,也就是 e -> a
- 所以 (g e) 返回 a
- f (g e) 就是
Reader e a - 再 run 一把最后得到 a
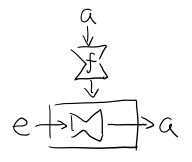
让我们来看看如何使用 Reader
import Control.Monad.Reader
data Environment = Env
{ fistName :: String
, lastName :: String
} deriving (Show)
helloworld :: Reader Environment String
helloworld = do
f <- asks firstName
l <- asks lastName
return "Hello " ++ f ++ l
runHelloworld :: String
runHelloworld = runReader helloworld $ Env "Jichao" "Ouyang"
这段代码很简单,helloworld 负责打招呼,也就是在名字前面加个 "Hello",而跟谁打招呼,这个函数并不关心,而单纯的是向 Environment 问 就好。
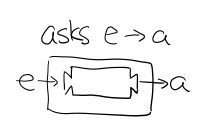
在运行时,可以提供给 Reader 的输入 Env fistname lastname。
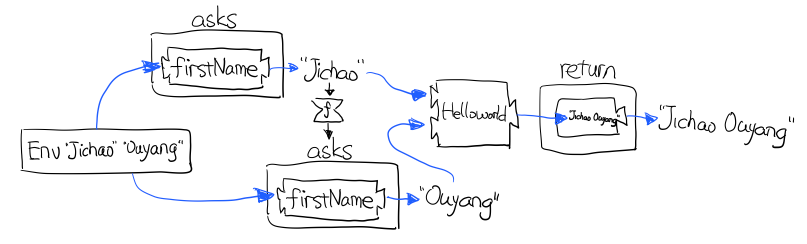
do notation
这可能是你第一次见到 do 和 <-. 如果不是,随意跳过这节。
- do 中所有 <- 的右边都是
Reader Environment String类型 - do 中的 return 返回类型也必须为
Reader Environment String asks firstName返回的是Reader Environment String类型,<-可以理解成吧 monadReader Environment的内容放到左边的 f, 所以 f 的类型是 String。
看起来像命令式的语句,其实只是 >>= 的语法糖,但是明显用do可读性要高很多。
helloworld = (asks firstName) >>=
\f -> (asks lastName) >>=
\l -> return "Hello " ++ f ++ l
Writer 光出进没有
除了返回值,计算会需要产生一些额外的数据,比如 log
此时就需要一个 Writter,其返回值会是一个这样 (result, log) 的 tuple
限制是 log 的类型必须是个 含幺半群
example :: Writer String String
example = do
tell "How are you?"
tell "I'm fine thank you, and you?"
return "Hehe Da~"
output :: (String, String)
output = runWriter example
-- ("Hehe Da~", "How are you?I'm fine thank you, and you?")
Writer 的定义更简单
newtype Writer l a = Writer { runWriter :: (a,l) }
里面只是一个 tuple 而已
- w 是 log
- a 是 返回值
看看如何实现 Writer monad
instance (Monoid w) => Monad (Writer w) where
return a = Writer (a,mempty)
(Writer (a,l)) >>= f = let (a',l') = runWriter $ f a in
Writer (a',l `mappend` l')
- return 不会有任何 log,l 是 monoid 的 mempty
- f 的类型为
a -> Writer l a runWriter $ f a返回(a, l)
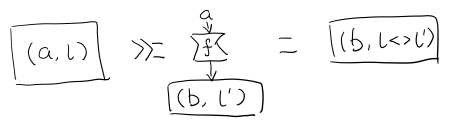
所以在 >>= 时,我们先把 f a 返回的 Writer run了,然后把两次 log mappend 起来。
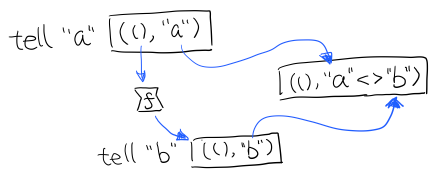
State 变化会有
跟名字就看得出来 State monad 是为了处理状态。虽然函数式编程不应该有状态,不然会引用透明性。但是,state monad并不是在计算过程中修改状态,而是通过描述这种变化,然后需要时在运行返回最终结果。这一点跟 Reader 和 Writer 这两个看起来是副作用的 IO 是一样的。
先看下 State 类型的定义
newtype State s a = State { runState :: s -> (a, s) }
可以看到 State 只包含一个 从旧状态 s 到新状态 s 和返回值 a 的 Tuple 的函数。
通过实现 Monad,State 就可以实现命令式编程中的变量的功能。
instance Monad (State s) where
return a = State $ \s -> (a,s)
(State x) >>= f = State $ \s -> let (v,s') = x s in
runState (f v) s'
return 很简单,就不用解释了。
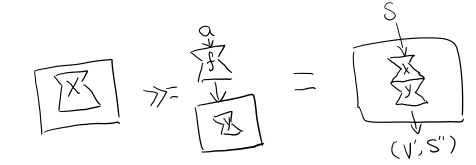
x 类型是 s -> (a, s) ,所以 x s 之后会返回 结果和状态。也就是运行当前 State,把结果 v 传给函数 f,返回的 State 再接着上次状态运行。
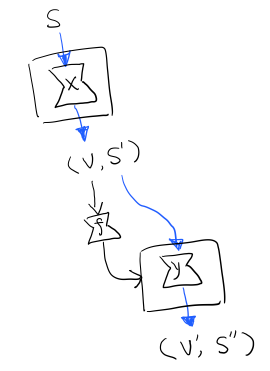
使用起来也很方便,State 提供 get put moidfy 三个方便的函数可以生成修改状态的State monad
import Control.Monad.Trans.State.Strict
test :: State Int Int
test = do
a <- get
modify (+1)
b <- get
return (a + b)
main = print $ show $ runState test 3
-- (7, 4)
Validation 检查检查
如果你有注意到,前面的 Either 可以用在处理错误和正确的路径分支,但是问题是错误只发生一次。
Validation 没有在标准库中,但是我觉得好有用啊,你可以在 ekmett 的 github 中找到源码
想象一下这种场景,用户提交一个表单,我们需要对每一个field进行验证,如果有错误,需要把错误的哪几个field的错误消息返回。显然如果使用 Either 来做,只能返回第一个field的错误信息,后面的计算都会被跳过。
针对这种情况, Validation 更适合
data Validation e a = Failure e | Success a
ADT定义看起来跟 Either 是一样的,不同的是 左边 Failure 是 含幺半群
含幺半群
monoid 首先得是 半群 ,然后再 含幺。
class Semigroup a where
(<>) :: a -> a -> a
(<>) = mappend
半群非常简单,只要是可以 <> (mappend) 的类型就是了。
含幺只需要有一个 mempty 的 幺元就行
class Monoid a where
mempty :: a
mappend :: a -> a -> a
比如 List 就是 Semigroup
instance Semigroup [a] where
(<>) = (++)
也是 Monoid
instance Monoid [a] where
mempty = []
mappend = (++)
Monoid 的 <> 满足:
- mempty <> a = a
- a <> b <> c = a <> (b <> c)
回到 Validation
现在让 Failure e 满足 Monoid,就可以 mappend 错误信息了。
instance Semigroup e => Semigroup (Validation e a) where
Failure e1 <> Failure e2 = Failure (e1 <> e2)
Failure _ <> Success a2 = Success a2
Success a1 <> Failure _ = Success a1
Success a1 <> Success _ = Success a1
下来,我们用一个简单的例子来看看 Validation 与 Either 有什么区别。
假设我们有一个form,需要输入姓名与电话,验证需要姓名是非空而电话是11位数字。
首先,我们需要有一个函数去创建包含姓名和电话的model
data Info = Info {name: String, phone: String} deriving Show
然后我们需要验证函数
notEmpty :: String -> String -> Validation [String] String
notEmpty desc "" = Failure [desc <> " cannot be empty!"]
notEmpty _ field = Success field
notEmpty 检查字符是否为空,如果是空返回 Failure 包含错误信息,若是非空则返回 Success 包含 field
同样的可以创建 11位数字的验证函数
phoneNumberLength :: String -> String -> Validation [String] String
phoneNumberLength desc field | (length field) == 11 = Success field
| otherwise = Failure [desc <> "'s length is not 11"]
实现 Validation 的 Applicative instance,这样就可以把函数调用lift成带有验证的 Applicative
instance Semigroup e => Applicative (Validation e) where
pure = Success
Failure e1 <*> Failure e2 = Failure e1 <> Failure e2
Failure e1 <*> Success _ = Failure e1
Success _ <*> Failure e2 = Failure e2
Success f <*> Success a = Success (f a)
- 失败应用到失败会 concat 起来
- 失败跟应用或被成功应用还是失败
- 只有成功应用到成功才能成功,这很符合验证的逻辑,一旦验证中发生任何错误,都应该返回失败。
createInfo :: String -> String -> Validation [String] Info
createInfo name phone = Info <$> notEmpty "name" name <*> phoneNumberLength "phone" phone
现在我们就可以使用带validation的 createInfo 来安全的创建 Info 了
createInfo "jichao" "12345678910" -- Success Info "jichao" "12345678910"
createInfo "" "123" -- Failure ["name cannot be empty!", "phone's length is not 11"]
Cont 接下来有
Cont 是 Continuation Passing Style 的 monad,也就是说,它是包含 cps 计算 monad。
先看一下什么是 CPS,比如有一个加法
add :: Int -> Int -> Int
add = (+)
但是如果你想在算法加法后,能够继续进行一个其他的计算,那么就可以写一个 cps版本的加法
addCPS :: Int -> Int -> (Int -> r) -> r
addCPS a b k = k (a + b)
非常简单,现在我们可以看看为什么需要一个 Cont monad 来包住 CPS 计算,首先,来看 ADT 定义
newtype Cont r a = Cont { runCont :: ((a -> r) -> r) }
又是一个同构的类型,Cont 构造器只需要一个 runCount,也就是让他能继续计算的一个函数。
完了之后来把之前的 addCPS 改成 Cont
add :: Int -> Int -> Cont k Int
add a b = return (a + b)
注意到 addCPS 接收到 a 和 b 之后返回的类型是 (Int -> r) -> r ,而 Cont 版本的 add 返回 Cont k Int
明显构造 Cont k Int 也正是需要 (Int -> r) -> r ,所以 Cont 就是算了 k 的抽象了。
instance Monad (Cont r) where
return a = Cont ($ a)
m >>= k = Cont $ \c -> runCont m $ \a -> runCont (k a) c
($ a) 比较有意思, 我们都知道 f $ g a 其实就是 f(g a), 所以 $ 其实就是一个 apply 左边的函数到右边表达式的中缀函数, 如果写成前缀则是
($ (g a) f). 是反的是因为 $ 是有结合, 需要右边表达式先求值, 所以只给一个 a 就相当于 ($ a) = \f -> f a
回到 Monad Cont…
Summary
第二部分食用部分也讲完了, 不知是否以及大致了解了monad的尿性各种基本玩法呢?通过这些常用的基本的 monad instance,解决命令式编程中的一些简单问题应该是够了。
不过,接下来还有更变态的猫,就先叫她 搞基 猫呢好了。
当然我又还没空全部写完,如果还有很多人预定 Gumroad 上的 Grokking Monad 电子书的话,我可能会稍微写得快一些。毕竟,写了也没人感兴趣也怪浪费时间的。不过,我猜也没几个人能看到这一行,就当是我又自言自语吧,怎么又突然觉得自己好分裂,诶~,为什么我要说又?